fircls (Signal Processing Toolbox)

Signal Processing Toolbox

fircls

Constrained least square FIR filter design for multiband filters.

Syntax

b = fircls(n,f,amp,up,lo)
fircls(n,f,amp,up,lo,'design_flag')

Description

b = fircls(n,f,amp,up,lo)generates a length n+1 linear phase FIR filter b. The frequency-magnitude characteristics of this filter match those given by vectors f and amp:

f is a vector of transition frequencies in the range from 0 to 1, where 1 corresponds to the Nyquist frequency. The first point of f must be 0 and the last point 1. The frequency points must be in increasing order.

amp is a vector describing the piecewise constant desired amplitude of the frequency response. The length of amp is equal to the number of bands in the response and should be equal to length(f)-1.

up and lo are vectors with the same length as amp. They define the upper and lower bounds for the frequency response in each band.

fircls always uses an even filter order for configurations with a passband at the Nyquist frequency. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, fircls increments it by 1.

fircls(n,f,amp,up,lo,'design_flag')enables you to monitor the filter design, where 'design_flag' can be:

'trace', for a textual display of the design error at each iteration step.

'plots', for a collection of plots showing the filter's full-band magnitude response and a zoomed view of the magnitude response in each sub-band. All plots are updated at each iteration step.

'both', for both the textual display and plots.

Examples

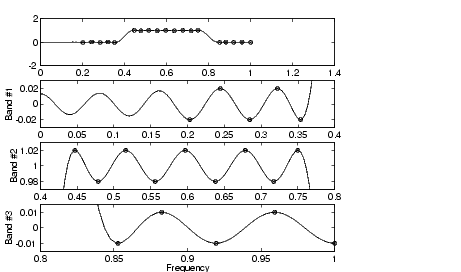
Design an order 50 bandpass filter.

n = 50;
f = [0 0.4 0.8 1];
amp = [0 1 0];
up = [0.02 1.02 0.01];
lo = [-0.02 0.98 -0.01];
b = fircls(n,f,amp,up,lo,'plots');  % Plot magnitude response

Note Normally, the lower value in the stopband will be specified as negative. By setting lo equal to 0 in the stopbands, a nonnegative frequency response amplitude can be obtained. Such filters can be spectrally factored to obtain minimum phase filters.

Algorithm

The algorithm is a multiple exchange algorithm that uses Lagrange multipliers and Kuhn-Tucker conditions on each iteration.

See Also

fircls1 Constrained least square filter design for lowpass and highpass linear phase FIR filters.

firls Least square linear-phase FIR filter design.

remez Parks-McClellan optimal FIR filter design.

`fircls1`	Constrained least square filter design for lowpass and highpass linear phase FIR filters.
`firls`	Least square linear-phase FIR filter design.
`remez`	Parks-McClellan optimal FIR filter design.

References

[1] Selesnick, I.W., M. Lang, and C.S. Burrus, "Constrained Least Square Design of FIR Filters without Specified Transition Bands," Proceedings of the IEEE Int. Conf. Acoust., Speech, Signal Processing, Vol. 2 (May 1995), pp. 1260-1263.

[2] Selesnick, I.W., M. Lang, and C.S. Burrus. "Constrained Least Square Design of FIR Filters without Specified Transition Bands." IEEE Transactions on Signal Processing, Vol. 44, No. 8 (August 1996).

fir2 fircls1