
Universidade
Federal do Paraná
Setor de
Tecnologia
Departamento
de Engenharia Elétrica
Turbo Code
Disciplina de Processamento digital
de sinais
Eduardo
Schnell e Schühli
Marcos Fábio Fuck
Marlon Luis Moser
Vilson Rodrigo Mognon
Curitiba, JANEIRO De 2002
Introdução
A crescente demanda para a troca de informações é uma característica da civilização moderna. A transferência da informação da sua fonte ao destino deve ser feita de maneira tal que a qualidade da informação recebida deve ser o mais parecida possível da informação transmitida. Um sistema típico de comunicação pode ser representado pelo diagrama de blocos da figura 1.
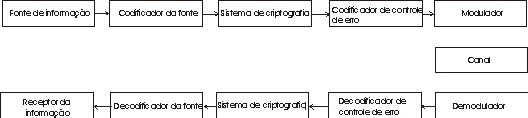
figura
1 - Sistema típico de telecomunicação [1]
Um dos
fatores que separam o mundo ideal do diagrama acima do real é os ruídos
presentes nos meios de transmissão da informações, os quais adicionam erros nas
transmissões digitais dificultando o recebimento da informação original no fim
do processo.
Neste
trabalho são discutidos os aspectos de controle de erro de um sistema de
telecomunicações, apresentando um dos mais eficientes métodos de correção de
erro, o Turbo Code.
Histórico
Por volta de 1947-1948 foi iniciado o estudo sobre teoria da informação por Claude Shannon. O principal resultado obtido pela “teoria matemática da comunicação” de Shannon é que a única maneira de conseguir a maior capacidade de armazenamento ou a mais rápida transmissão através de um canal de comunicação é através do uso de poderosos sistemas de correção de erro. Shannon traçou uma curva com a máxima taxa de transmissão possível em um canal. Na mesma época Richard Hamming descobriu e implementou um código de correção de erro de um bit.[9]
Em 1960
Gustave Solomon descobriu como construir códigos de correção de erro que podem
corrigir um número arbitrário de bits ou bytes. Porém ainda não tinha uma
maneira de decodificar o código. Hoje o processos de correção de erro
reed-solomon é utilizado na gravação de arquivos de música no formato DAT
(Digital áudio tape), DVD, CD, comunicação de satélites, televisão digital,
modems de alta velocidade como ADSL, xDSL, celulares, etc.[9]
Em 1961
foi escrito o primeiro livro por Wesley Peterson.[9]
Em 1968
Elwyn Berlekamp e James Massey descobriram algorítimos necessários para a
decodificação para códigos de correção de múltiplos bits.[9]
Em 1993
foi introduzido o que hoje é considerado como o mais eficiente código para
correção de erros (FEC- Forward Error Correction), o turbo code. O conceito do
Turbo Code foi introduzido na conferência ICC’93 em Geneva por C. Berrou da
ENST de Bretagne. No paper Berrou considerava a decodificação iterativa de dois
códigos de sistemas recursivos convolucionais (RSC) concatenados em paralelo
através de um interleaver não uniforme. Para a decodificação ele usava um SISO
(soft Input/ Soft Output) decodificador baseado em MAP (Maximum a Posteriori)
algorithm.[8]
Em 1994,
Ramesh Pyndiah também da ENST de Bretagne propôs um turbo code baseado em
blocos. Para este turbo code ele usava um decodificador iterativo de dois BCH
códigos concatenados em série através de um interleaver não uniforme. Para a
decodificação era proposto um novo SISO decodificador para blocos.[8]
Até hoje
foram publicadados vários papers envolvendo este tema, que revolucionou a correção
de erro.
Controle
de erro
Da
teoria de codificação, sabe-se que incrementando-se o tamanho da
“palavra-código” ou da memória do codificador, pode-se atingir maior proteção
ou ganho de codificação. Ao mesmo tempo a complexidade de um algoritmo típico
de decodificação como os Algoritmos Decodificadores de Máxima Probabilidade
(ADMP) aumenta exponencialmente com a memória codificadora e os algoritmos
tornam-se de difícil implementação. A crescente capacidade de correção de erro
de códigos longos requer um alto esforço computacional no decodificador. Isto
levou à pesquisas para novos esquemas de códigos que possam vir a substituir os
ADMP com técnicas decodificadoras simplificadas.[5]
A nova
classe de “códigos turbo” – turbo codes – codifica a mesma informação duas
vezes, mas em uma ordem diferente. Quanto mais misturada esteja a primeira
informação codificada da segunda, mais não-relacionada estará a troca de
informação entre os decodificadores. Esta é uma das idéias principais (ou
idéia-chave) que permite um aperfeiçoamento contínuo na capacidade de correção
quando a iteração do processo de decodificação se inicial. [3]
Em uma
aproximação tradicional, o bloco demodulador da figura 1 toma uma difícil
decisão do símbolo recebido e repassa ao bloco decodificador de controle de
erro. Isto se equivale a decidir qual entre dois valores lógicos – digamos 0 e
1 – foi transmitido. Nenhuma informação foi passada a respeito de quão factível
a decisão seria. Resultados melhores são obtidos quando o sinal analógico
quantificado recebido for passado diretamente ao decodificador.[3]
Algoritmos
de decisão de saída suaves (SISO) fornecem como saída um número real que é uma
medida da probabilidade de erro em se decodificar um bit em particular. Isto
também pode ser interpretado como uma medida de quão realizável seria a decisão
difícil tomada pelo decodificador. Esta informação extra é muito importante
para o próximo estágio em um processo iterativo de decodificação, como será
mostrado mais tarde. Há duas categorias importantes para os algoritmos suaves
de decisão de saída. A primeira categoria inclui os Algoritmos Decodificadores
de Máxima Probabilidade que minimizam a probabilidade de erro de símbolo, como
o Algoritmo Máximo a Posteriori (MAP). A segunda categoria inclui os Algoritmos
Decodificadores de Máxima Probabilidade que minimizam a probabilidade de erro
de palavra ou seqüência, como o algoritmo Viterbi ou o Algoritmo Viterbi de
Saída Suave (SOVA).[3]
Turbo
Code
Um Turbo Codes é uma combinação de dois
codificadores simples. A entrada é um bloco de K bits de informação. Os dois
codificadores geram símbolos de paridade de dois códigos simples convolucionais
recursivos, cada qual com um
pequeno número de estados. Os bits de informação são também enviados sem codificação.
A chave da inovação do Turbo Codes é
um interleaver P, o qual permuta os bits de informação K originais antes
de colocá-los no segundo codificador. O permutador P permite que a seqüência de
entrada para um codificador produza palavras de bits de baixo nível, geralmente
causará que o outro codificador produza palavras de bits de alto nível. Assim,
mesmo que os códigos constituintes sejam individualmente fracos, a combinação é
surpreendentemente poderosa. O código resultante tem facilidades similares a um
bloco de códigos “aleatórios” com K bits de informação.[2]
O bloco
de códigos aleatórios é conhecido por conseguir uma performance próxima ao
limite de Shannon enquanto K torna-se
maior, porém o preço será provavelmente complexos algoritmos de decodificação. Turbo Codes imitam a boa performance
dos códigos aleatórios (para um grande K) utilizando um algoritmo decodificador
interativo baseado em decodificadores simples individuais combinados para a
simples constituição dos códigos. Cada decodificador constituinte envia uma
estimativa posteriori em probabilidades de bits decodificados para o
outro decodificador, e utiliza os bits estimados correspondentes do outro
decodificador como um probabilidade a priori.
Os bits de informação não codificados (corrompidos por um canal de
interferência) são disponibilizados para cada decodificador para serem as novas
probabilidades a priori. Os
decodificadores usam o “MAP” (Maximum a
Posteriori) como algoritmo decodificador de bits, o qual requer o mesmo
número de estados como o bem conhecido algoritmo Viterbi. O Turbo Code intera entre as saídas dos dois
decodificadores até alcançar a convergência satisfatória. A saída final é uma
versão refinada e quantizada das estimativas prováveis de um dos
decodificadores.[2]
Estrutura
do Turbo Code
Na
figura 2 apresenta-se um codificador turbo genérico em duas dimensões. A
seqüência de entrada dos bits de informação é organizada em blocos de tamanho
N. O primeiro bloco de dados será codificado pelo bloco ENC- que é
um codificador sistemático recursivo de meia taxa. O mesmo bloco de bits de
informação é inserido com o interleaver INT, e codificado por ENC|
que também é um codificador sistemático recursivo de meia taxa. O bit
codificado produzido pelo codificador é a saída de cada bloco codificador.[1]
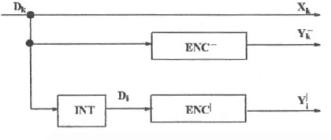
Figura 2
– Codificador de taxa 1/3
Devido à
similaridades com os códigos produzidos, o bloco ENC- é visto como a
dimensão horizontal e o ENC| como a dimensão vertical. O bloco interleaver
INT, rearranja a ordem dos bits de informação para a entrada do segundo
codificador. O principal propósito do interleaver é incrementar a
distância mínima do turbo code tal que após a correção em uma dimensão os erros
restantes possam vir a ser padrões de erro corrigíveis na segunda dimensão.[1]
Ignorando-se
o momento de atraso de cada bloco, assumimos os dois codificadores de dados de
saída simultaneamente. Isto é um turbo code de taxa 1/3, onde a saída do
codificador turbo é o trio (Xk, Yk-, Yk|).
Este trio é então modulado para transmissão através do canal de comunicação,
sendo tomado como o canal Aditivo de Ruído Branco Gaussiano (AWGN). Sendo o
código sistemático, Dk=Xk representa os dados de entrada
em no tempo k. Yk- e Yk| são os
bits de paridade no tempo k.[1]
Estes
dois codificadores não precisam ser idênticos. Na figura 2 os dois
codificadores são codificadores sistemáticos de taxa ½ com apenas o bit de
paridade mostrado. Os bits de paridade podem ser multiplexados como na figura
3, sendo isto feito por uma chave multiplexadora, para se obter taxas de
codificação maiores.[1]
O
símbolo D representa um flip-flop D (o clock não é mostrado) e o símbolo +
representa uma porta ou-exclusivo.
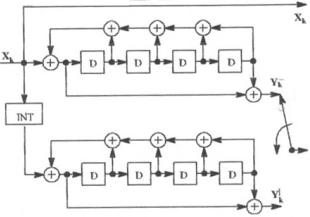
Figura 3
– Codificador de taxa 1/2 [1]
A figura 3 mostra uma implementação particular de um turbo code de duas dimensões usando Códigos Sistemáticos Recursivos (CSR). Taxas menores de codificação podem ser usadas usando menos circulações ou mais interleavers e blocos codificadores como mostrado na figura 4 para um turbo code de n dimensões. A vantagem de se usar mais interleavers ficará mais clara adiante, onde se apresenta a performance de turbo codes de baixas taxas.
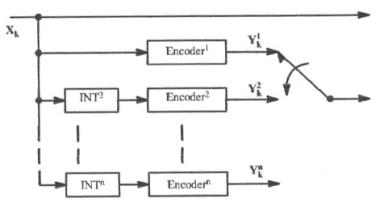
Figura 4
– Codificador de baixa taxa [1]
O codificador turbo básico tem dois
codificadores convolucionais separados por um interleaver randômico.
Esta estrutura é chamada de Código Convolucional Concatenado Paralelo (CCCP)
desde que o mesmo fluxo de informação é codificado duas vezes, em paralelo,
usando as seqüências direta e permutada dos bits de informação. [1]
Uma
alternativa óbvia é inserir a saída de um codificador e recodificá-lo. A isto
damos o nome de Código Convolucional Concatenado Serial (CCCS).
Usando o
conceito de interleaver uniforme, há uma grande diferença entre o ganho
de interleavers entre as estruturas CCCP e CCCS. Para as estruturas CCCP
o ganho do interleaver é definido por um fator multiplicativo N1
no limiar do BER (taxa de erro de bit). Para estruturas CCCS, o ganho do interleaver
é definido por N-(do+1) x 0.5 onde do é a distância livre
do código mais externo (por exemplo, codificador 1 na figura 5 ).

Figura 5
– Codificador convolucional serial [1]
Interleaver
O
projeto do interleaver é um fator chave que determina a boa performance
do turbo code. Alguns tipos de interleavers usados em turbo codes são apresentados
nas próximas seções.
Interleaver
“Linha-Coluna”
O interleaver
mais simples é uma memória em que os dados são escritos ao longo de uma linha e
lidos ao longo de uma coluna. Este é chamado de interleaver
“linha-coluna” e pertence à classe dos interleavers em “bloco”. [1]
Interleaver
Par-Ímpar
Descobriu-se
que para um codificador de meia taxa como mostrado na figura 3, um tipo
particular de interleaver chamado de “par-ímpar”, fornece melhoras
significativas quando usado em um projeto de codificador turbo. Assumimos que
temos uma seqüência randômica de entrada de dados binários com um codificador
de taxa ½ e armazenamos apenas os bits ímpares codificados. [1]
Interleaver
“Símile”
No interleaver
par-ímpar cada bit de informação está associado com um somente um bit
codificado. Nesta maneira a capacidade de correção é distribuída uniformemente
através de todos os bits de informação. Agora vamos impor uma outra restrição
no projeto do interleaver: depois de codificar ambas as seqüências dos
bits de informação (a original e a do interleaver), o estado de ambos os
codificadores do turbo code devem ser os mesmos. Isto permite apenas uma parte
a ser acrescida aos bits de informação, que torna ambos os codificadores para o
mesmo estado zero. Isto explica o porquê de ser chamado de interleaver
de comparação.
O interleaver
de comparação devem realizar a inserção dos bits em cada seqüência particular
para direcionar o codificador para o mesmo estado ao qual ocorre sem inserção.
Desde que ambos os codificadores terminem em um mesmo estado, precisamos que
apenas uma parte dirija ambos os codificadores para o estado zero ao mesmo
tempo.[1]
Interleaver “Frame”
O
codificador RSC pode ser caracterizado como um gerador polinomial de período L.
Neste caso os N bits de informação a serem inseridos são armazenados duas vezes
em uma memória de tamanho 2N, em endereços tal que suas leituras subseqüentes
para codificação é separada no tempo por um número de períodos que é um
múltiplo de L. Deste jeito, se o codificador inicia no estado zero, terminará
no estado zero sem a necessidade de parte de bits.[1]
Interleaver
Pseudo-randômico
Os interleavers
pseudo-randômicos são definidos por um gerador numérico pseudo-randômico ou uma
tabela onde todos os inteiros de 1 a N (o tamanho do bloco a ser inserido)
podem ser gerados. [1]
Interleaver
Uniforme
É a
média de todos os interleavers possíveis. Um interleaver uniforme de tamanho k
é um dispositivo probabilístico que mapeia a seqüência de todos os distintas
permutações com igual probabilidade.[1]
De todos
os exemplos acima de projeto de interleaveres fica claro que o papel do interleaver
é permitir aos decodificadores realizar estimativas não-relacionadas de valores
suaves de um mesmo bit de informação. Quanto menos correlacionadas estejam duas
alternativas, melhor a convergência do algoritmo iterativo de
decodificação.
Performance
A
performance do sinal de saída dos códigos concatenados do Turbo Codes são usados pelo DSN desde o Voyager até o Neptune.
Por exemplo, turbo codes construídos
de dois códigos constituídos de 16 estados podem conseguir uma taxa de erro de
bit de 10-5 para o SNRs
mostrados no gráfico 1 para turbo codes
com taxas de ½, ¼ e 1/6. O resultado também mostra os
SNRs requeridos para uma taxa similar de códigos concatenado DSN usados pela Voyager, Galileo e Cassini. Todos os
códigos concatenados DSN usam um códigos de saída Reed-Solomon poderoso em conjunto com uma convolução com os códigos
de entrada, visto que os turbo codes
são supostos para operar sem concatenação. Para Galileo, duas comparações são mostradas: como planejado
originalmente, e como reprogramada para pequenas taxas de dados após a falha de
abertura das antenas de alto ganho. A
performance das melhorias conseguidas pelo turbo
codes são de aproximadamente 1,5 dB, 1,3 dB e 1,0 dB, com relação a Voyager, Galileo (planejado), e Cassini codes. Há também uma melhoria
de 0,7 dB com relação ao redesigned Galileo code, o qual requer múltiplas
interações entre a entrada e a saída dos decodificadores. [7]
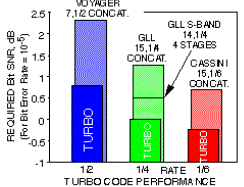
Gráfico
1 – Performance do Turbo Code [7]
Além de
oferecer uma melhora no desempenho, os decodificadores turbo são menos complexos que os decodificadores concatenados do Galileo e do Cassini. O tempo de
decodificação é proporcional ao número de estados e ao número de interações, a
menos que exista um hardware especial seja utilizado para processamento
paralelo em alguns ou em todos os estados. Os resultados mostram que o número
de estados para os decodificadores turbo é de menor magnitude que para os
decodificadores Galileo e Cassini, e
este mais do que os offsets o modesto
número de interações requiridas. O tamanho do Interleaver impacta no buffer exigido e no delay de
decodificação, mas não no tempo de decodificação: ele é um determinante primário
do desempenho do turbo code (maior e
melhor), contudo o desempenho fenomenal mostra que o resultado é conseguido com
interleavers que não são muito
maiores que os frames intercalados
dos dados do tradicional sistema de concatenação DSN.[7]
No gráfico 2 temos a comparação do desempenho dos métodos de Reed-Solomon/viterbi, Turbo Product Code, Turbo Convolucional Code. Em azul podemos observar o limite teórico determinado pela lei de Shannon e em rosa a transmissão não codificada, observa-se que o turbo code tem desempenho muito superior ao de Reed-Solomon/viterbi, dando um ganho significativo em relação ao canal original, aproximando-se bastante do limite teórico.
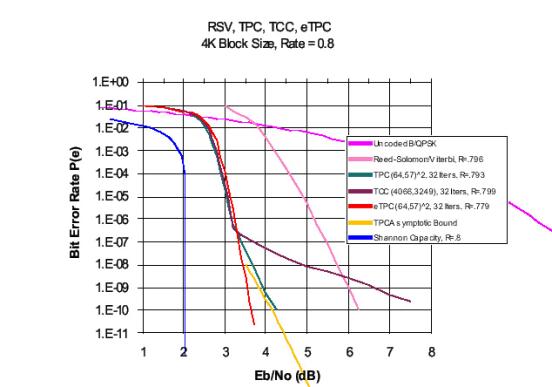
Gráfico
2 – Comparação de performance [4]
Na tabela 1 podemos observar outra comparação entre os métodos de Turbo Product Code (TPC), Reed-Solomon, Viterbi, Reed-Solomon/Viterbi, Turbo Convolucional Code (TCC). Outra variável importante analisada nesta tabela é a complexidade do códico, observa-se que o Turbo Convolucional Code é sempre mais simples e seus resultados são quase sempre superiores.
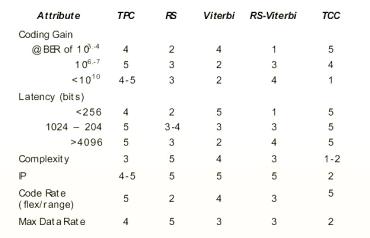
Tabela 1
– Comparação de performance [4]
No gráfico 3 observamos a comparação de desempenho sobre o tráfego de dados no protocolo ATM.
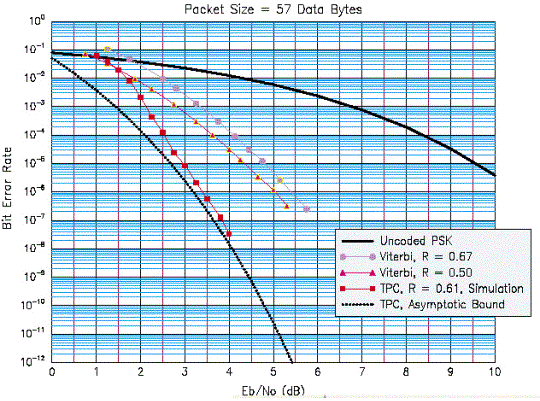
Gráfico
3 – Comparação de performance em ATM [4]
No gráfico 4 observamos a comparação de desempenho sobre o tráfego de informações no padrão MPEG.
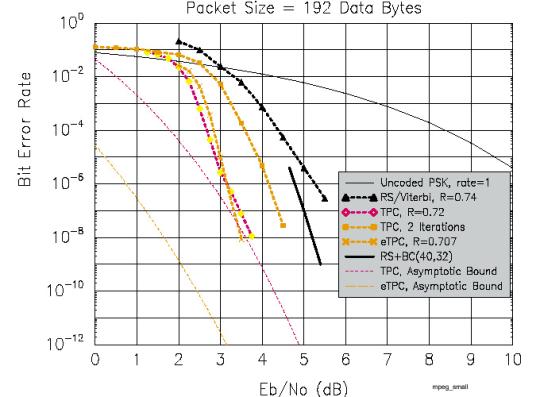
Gráfico
4 – Comparação de performance em MPEG [4]
Exemplo
Na
figura 6 temos a figura original e ela adicionada de ruído gaussiano branco
Na
figura 7 temos a figura corrigida por uma iteração do turbo code e na outra a
segunda iteração. Pode-se observar que já na primeira iteração o número de
ruído é bem pequeno, e que na segunda elas quase desapareceram.


Figura 6
– Figura original e a mesma com ruído branco gaussiano [6]


Figura 7
– Figura corrigida por Turbo Code com uma e duas iterações [6]
Conclusão
A
transmissão de dados hoje está presente cada vez mais em nossa sociedade, e
junto com ela cresce a necessidade de que seja feita com perfeição. Para atingir
esta melhoria é necessário que se faça uso de sistemas para que consiga-se
corrigir estes erros, e enquanto tivermos meios de transmissão não ideais eles
se farão necessários.
Quando
falamos em transmissão de dados não podemos nos limitar a transmissão
tradicional, utilizando como meio o ar ou um par fios. Um bom exemplo para
quebrar este modelo é o do CD, ou DVD, aonde os dados estão gravados
codificados na mídia e os erros são adicionados quando não é possível a leitura
de alguma parte da mídia por risco ou outro motivo. Os DVD’s assim como outras
aplicações multimídia utilizam de um código de correção de erro chamado
Reed-Solomon.
Através
deste trabalho tentamos provar que o turbo code é a ferramenta ideal para a
maioria dos casos em correção de erro, pois além de apresentar desempenho
superior é de fácil implementação, e só não está mais difundido porque sua
descoberta é muito recente (1993).
Pode-se
fazer a pergunta: Para que utilizar correção de erro se eu já tenho um
desempenho suficiente sem utiliza-lo?
Um ganho
em códigos de 3dB pode:
·
Reduzir a banda necessária em 50%
·
Reuzir o tamanho da antena em 30%
·
Reduzir a potência de transmissão em 50%
·
Aumentar o tamanho dos dados a serem transmitidos em 100%
[4]
Usando o
turbo code, com pouco esforço pode-se melhorar a qualidade da transmissão e
diminuir custos.
Bibliografia
[1] S.S.Pietrobon “Turbo Codes: A Tutorial on a New
Class of Powerful Error Correcting Coding Schemes” Institute for
Telecommunication Research;
[2] J.Hagenauer “The Turbo Principle: Tutorial
Introduction and State of the Art” Technical University of Munich;
[3] C.Berrou “Near Optimum Error Correcting Coding and
Decoding: Turbo-Codes” IEEE Transaction on Communications. Vol 44 No 10.
October 1996.
[4] D. Williams “Turbo Product Code Tutorial”
[5] http://user-www.ie.cuhk.edu.hk/~chankm6/TurboCode/contents.html
acessado em 11/01/2002
[6] http://www.softdsp.com/sds_fec.htm
acessado em 23/01/02
[7] http://www331.jpl.nasa.gov/public/TurboForce.GIF
acessado em 23/01/02
[8] http://www-sc.enst-bretagne.fr/historic.html
acessado em 24/01/02
[9] http://members.aol.com/mnecctek/faqs.html#hist
acessado em 24/01/02