Transformada Discreta do Coseno

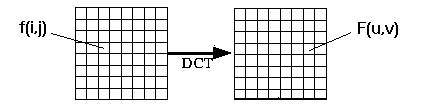
Os dados da imagem que estão em forma espacial, através dos sistemas de cores RGB ou YUV, deve ser transformado para o domínio da freqüência, e o artificio matemático usado é a DCT. Na figura abaixo ilustra essa passagem:

Agora que a imagem foi transformada em uma matriz 8x8 e está no esquema de cores desejado(YUV) os coeficientes da Transformada Discreta do coseno podem ser determinadas. A função matemática para a transformada DCT bidimensional é:

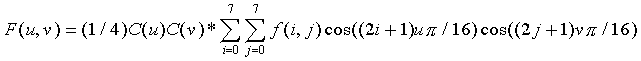
Para efeitos de decodificação temos a seguinte expressão para a equação da transformada inversa:

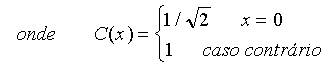
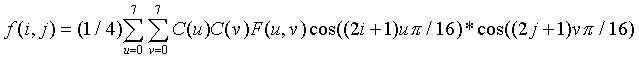
Podemos interpretar as componentes u e v como sendo freqüências espaciais horizontal e vertical, respectivamente. Deste modo, podemos chamar o coeficiente correspondente a u=0 e v=0 (F[0,0]) de componente DC do bloco. Os outros 63 coeficientes são denotados coeficientes AC por não serem relacionados com as freqüências espaciais nulas. Em imagens reais, a maior parte da energia está geralmente concentrada nos componentes de baixa freqüência. Logo, utilizando a DCT conseguimos uma concentração da energia do bloco no coeficiente DC e nos coeficientes AC de baixas freqüências.

Numa imagem típica, muitos dos coeficientes terão valor zero ou próximos de zero. Estes componentes serão descartados no processo de compactação de dados.

Note-se que a DCT em si não compacta os dados. A análise dos valores resultantes da DCT é que permite escolher os dados que podem ser descartados, sem perda visível de qualidade de imagem.